Atšķirība starp T-testu un ANOVA
 Share
Share
 T-testa un ANOVA vidusdaļā ir plānota robežu robeža, t.i., ja jāsalīdzina tikai divu grupu populācijas vidējie lielumi. t-tests tiek izmantots, bet, ja jāsalīdzina vairāk nekā divu grupu līdzekļi, ANOVA ir vēlama.
T-testa un ANOVA vidusdaļā ir plānota robežu robeža, t.i., ja jāsalīdzina tikai divu grupu populācijas vidējie lielumi. t-tests tiek izmantots, bet, ja jāsalīdzina vairāk nekā divu grupu līdzekļi, ANOVA ir vēlama.
T-tests un variācijas analīze, saīsināti kā ANOVA, ir divas parametriskas statistikas metodes, kuras izmanto hipotēzes pārbaudei. Tā kā tie ir balstīti uz vispārpieņemto pieņēmumu, piemēram, parasti jāsadala populācija, no kuras tiek ņemti paraugi, dispersijas viendabīgums, nejauša datu atlase, novērojumu neatkarība, atkarīgā mainīgā lieluma mērīšana proporcijas vai intervāla līmenī, cilvēki bieži tos nepareizi interpretē. divi.
Šeit ir raksts, kas jums piedāvāts, lai saprastu būtisko atšķirību starp t-testu un ANOVA, apskatiet.
Saturs: T-tests Vs ANOVA
- Salīdzināšanas tabula
- Definīcija
- Galvenās atšķirības
- Secinājums
Salīdzināšanas tabula
| Salīdzināšanas pamats | T-tests | ANOVA |
|---|---|---|
| Nozīme | T-tests ir hipotēzes tests, ko izmanto, lai salīdzinātu divu populāciju vidējos rādītājus. | ANOVA ir statistikas paņēmiens, ko izmanto, lai salīdzinātu vairāk nekā divu populāciju vidējos rādītājus. |
| Testa statistika | (x ̄-µ) / (s / √n) | Starp parauga dispersiju / parauga dispersijas robežās |
T-testa definīcija
T-testu apraksta kā statistisko testu, kurā pārbauda, vai divu paraugu populācijas vidējie lielumi ievērojami atšķiras viens ar otru, izmantojot t-sadalījumu, ko izmanto, ja standarta novirze nav zināma, un parauga lielums ir mazs. Tas ir rīks, lai analizētu, vai abi paraugi ir ņemti no vienas populācijas.
Pārbaudes pamatā ir t-statistika, kas pieņem, ka mainīgais lielums parasti ir sadalīts (simetrisks zvanveida formas sadalījums) un vidējais lielums ir zināms, un populācijas dispersija tiek aprēķināta no parauga.
T-testā nulles hipotēze izpaužas kā H0: µ (x) = µ (y) pret alternatīvo hipotēzi H1: µ (x) ≠ µ (y), kur µ (x) un µ (y) apzīmē populācijas vidējo vērtību. T-testa brīvības pakāpe ir n1 + n2 - 2
ANOVA definīcija
Variances analīze (ANOVA) ir statistikas metode, ko parasti izmanto visās situācijās, kad jāveic salīdzinājums starp vairāk nekā diviem populācijas līdzekļiem, piemēram, ražas no vairākām sēklu šķirnēm raža. Tas ir svarīgs analīzes rīks pētniekam, kas viņam ļauj vienlaikus veikt pārbaudi. Kad mēs izmantojam ANOVA, tiek pieņemts, ka paraugs tiek ņemts no normāli sadalītas populācijas un populācijas dispersija ir vienāda.
ANOVA kopējais variāciju daudzums datu kopā tiek sadalīts divos veidos, t.i., summai, kas piešķirta nejaušībai, un summai, kas piešķirta noteiktiem cēloņiem. Tās pamatprincips ir pārbaudīt variācijas starp iedzīvotāju vidējiem lielumiem, novērtējot variāciju daudzumu grupas posteņos, proporcionāli variāciju lielumam starp grupām. Paraugā dispersija rodas nejauši neizskaidrojamu traucējumu dēļ, turpretī atšķirīga attieksme var izraisīt parauga dispersiju.
Izmantojot šo paņēmienu, mēs pārbaudām nulles hipotēzi (H0), kur visi populācijas līdzekļi ir vienādi, vai alternatīva hipotēze (H1), kur vismaz viens populācijas vidējais ir atšķirīgs.
Galvenās atšķirības starp T-testu un ANOVA
Būtiskās atšķirības starp T-testu un ANOVA ir sīki apskatītas šādos punktos:
- Hipotēzes testu, ko izmanto, lai salīdzinātu divu populāciju vidējos lielumus, sauc par t-testu. Statistikas paņēmiens, ko izmanto, lai salīdzinātu vairāk nekā divu populāciju vidējos rādītājus, ir pazīstams kā dispersijas analīze vai ANOVA.
- T-testa testa statistika ir:
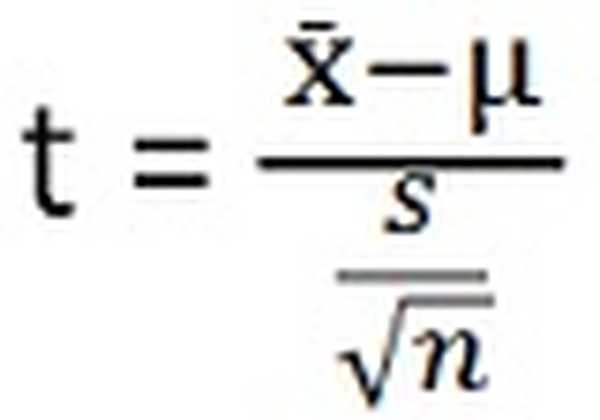 ANOVA testa statistika ir:
ANOVA testa statistika ir: 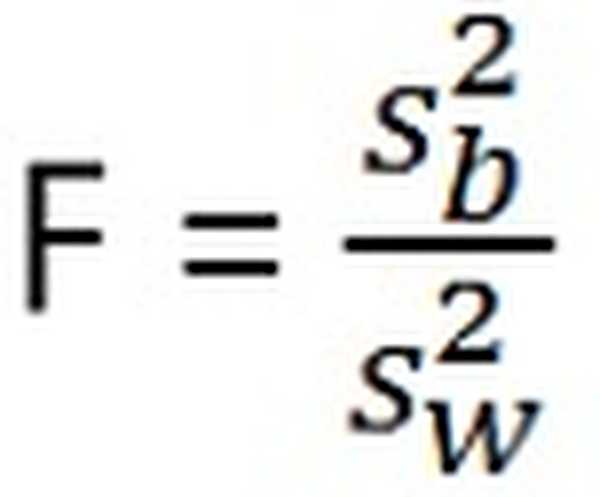
Secinājums
Pārskatot iepriekš minētos punktus, var teikt, ka t-tests ir īpašs ANOVA tips, ko var izmantot, ja mums ir tikai divas populācijas, lai salīdzinātu viņu līdzekļus. Lai gan kļūdu iespējamība var palielināties, ja tiek izmantots t-tests, kad vienlaikus jāsalīdzina vairāk nekā divi populāciju vidējie lielumi, tieši tāpēc tiek izmantota ANOVA
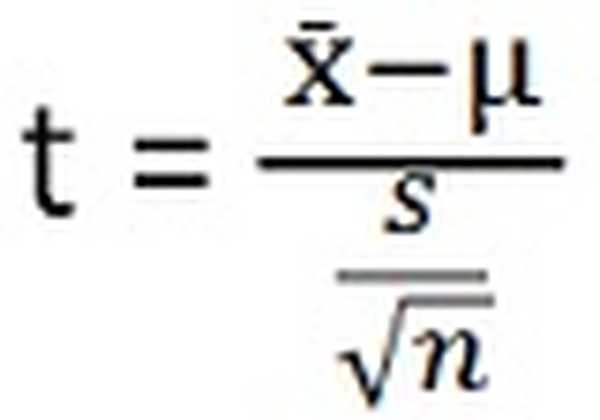 ANOVA testa statistika ir:
ANOVA testa statistika ir: